Si consideri la funzione polinomiale
Tale polinomio ammette solo due
radici reali 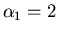 ed
ed 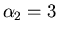 . Si produca con gnuplot
la figura pol.ps scegliendo un intervallo
. Si produca con gnuplot
la figura pol.ps scegliendo un intervallo 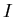 (sufficientemente piccolo) che
le contanga entrambe.
Si identifichino poi due sottointervalli contigui (
(sufficientemente piccolo) che
le contanga entrambe.
Si identifichino poi due sottointervalli contigui (![$I_1=[a_0,b_0]$](img5.gif) e
e
![$I_2=[b_0,c_0]$](img6.gif) ) dell'intervallo
) dell'intervallo 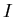 che contengano ognuno una sola delle
due radici e si producano le due figure che contengano la funzione
che contengano ognuno una sola delle
due radici e si producano le due figure che contengano la funzione 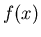 relativa ai due intervalli
relativa ai due intervalli 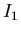 ed
ed 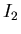 (files
polrad1.ps e polrad2.ps).
Si applichi a ciascun intervallo
(files
polrad1.ps e polrad2.ps).
Si applichi a ciascun intervallo 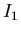 ed
ed 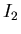 il metodo di bisezione, sino a raggiungere una tolleranza sull'ampiezza dell'intervallo di
il metodo di bisezione, sino a raggiungere una tolleranza sull'ampiezza dell'intervallo di 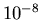 .
.
Si memorizzino su due file ( bisrad1.dat e bisrad2.dat)
le due successioni
ottenute indicando come ascissa gli indici delle iterazioni
(a partire da  ) e come ordinata il valore di
) e come ordinata il valore di 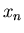 (punto medio
dell'intervallo ottenuto all'iterazione
(punto medio
dell'intervallo ottenuto all'iterazione 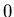 ).
).
Si
producano due figure ( bisrad1.ps e bisrad2.ps) utilizzando i due file dati precedenti.
Si consideri poi il seguente metodo di punto fisso
e si ritrovino le soluzioni graficamente producendo in 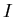 la figura
fisso.ps.
la figura
fisso.ps.
Si applichi poi il metodo
di punto fisso precedentemente definito, a partire dal punto
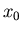 =1.5, sino a raggiungere una tolleranza sulla differenza di due iterate
successive di
=1.5, sino a raggiungere una tolleranza sulla differenza di due iterate
successive di 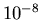 . Il metodo converge alla radice
. Il metodo converge alla radice 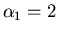 con
ordine 4.
con
ordine 4.
Si memorizzi su di file ( fisso.dat)
la successione
ottenuta con tale metodo.
Si rappresentino sulla stessa figura ( iter.ps) le due successioni
bisrad1.dat e fisso.dat ottenute con il precedente metodo
di bisezione e con il metodo di punto fisso.