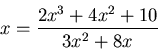Calcolo Numerico
Corso di laurea in Ingegneria Chimica e del Materiali
Prof. Michela Redivo Zaglia
Laboratorio 16 maggio 2003
ATTENZIONE: I programmi che calcolano le successioni devono utilizzare delle SUBROUTINE generali
relative ai vari metodi (bisezione, Newton, punto fisso, ecc,).
Si deve utilizzare sempre la doppia precisione per variabili e costanti e l'uso di un formato in modo
che i files di uscita contengano almeno 16 cifre decimali per ogni numero reale.
 Esercizio 1
Esercizio 1
Si consideri la funzione (già utilizzata nel laboratorio dell'8 aprile 2003)
che ha le tre soluzioni che erano state indicate con
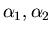 ed
ed 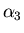 (in senso crescente).
Si applichi il metodo di Newton, a partire dal punto iniziale
(in senso crescente).
Si applichi il metodo di Newton, a partire dal punto iniziale
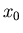 =10.0, sino a raggiungere una tolleranza sulla differenza di due iterate
successive di
=10.0, sino a raggiungere una tolleranza sulla differenza di due iterate
successive di 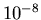 .
.
Con tale punto iniziale il metodo di punto fisso converge. A quale radice?
Si scrivano su di un file esterno due colonne di dati: nella prima si
inserisca il numero dell'iterazione (a partire da 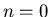 ), e nella seconda il valore ottenuto con il metodo di Newton.
Considerato il metodo del punto fisso del laboratorio dell'8 aprile 2003,
), e nella seconda il valore ottenuto con il metodo di Newton.
Considerato il metodo del punto fisso del laboratorio dell'8 aprile 2003,
con punto
iniziale scelto in modo che converga alla stessa radice del metodo di Newton, ed il
metodo di bisezione relativo all'intervallo che contiene la stessa soluzione,
si produca una figura riassuntiva che abbia in ascisse l'indice dell'iterata
e in ordinata i valori assunti dalla successione delle iterate per i tre metodi considerati.
Si rappresentino su di un'altra unica figura
anche le tre curve (relative a Bisezione, Newton e punto fisso)
con ordinate pari al
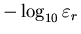 e sulle ascisse l'indice delle iterate delle successioni.
e sulle ascisse l'indice delle iterate delle successioni.
Nel programma che calcola il
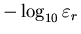 , si controlli
che l'errore assoluto di ogni iterata rispetto alla soluzione esatta
sia non nullo, per evitare divisioni per lo zero.
, si controlli
che l'errore assoluto di ogni iterata rispetto alla soluzione esatta
sia non nullo, per evitare divisioni per lo zero.
Si applichino gli algoritmi di stima del capitolo 3, sezione 3.15.2,
per ritrovare numericamente l'ordine di convergenza di
ognuno dei 3 metodi considerati.
 Esercizio 2
Esercizio 2
 Esercizio 3
Esercizio 3
 Esercizio 1
Esercizio 1
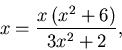
 Esercizio 2
Esercizio 2
 Esercizio 3
Esercizio 3