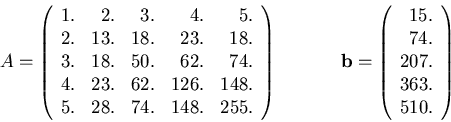Calcolo Numerico
Prof. Michela Redivo Zaglia
Raccolta di esercizi sui SISTEMI DI EQUAZIONI LINEARI
 Esercizio 1
Esercizio 1
- Si scrivano due subroutine per implementare la risoluzione di
un sistema triangolare superiore e di un sistema triangolare inferiore (gli algoritmi si trovano
sul libro di testo, sezioni 4.17.1 e 4.17.2)
-
Si scrivano poi due programmi di utilizzo di tali subroutine,
provandoli con i sistemi:
entrambi con soluzione
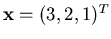 .
.
 Esercizio 2
Esercizio 2
- Usando la doppia precisione, si scrivano due subroutine per implementare il
Metodo di Gauss (una senza pivoting e l'altra con pivoting), come indicato nel libro di testo
(sezioni 4.17.3 e 4.17.4).
- Si scrivano poi i programmi ed, utilizzando anche la subroutine sviluppata
nell'Esercizio 1 (risoluzione di un sistema
triangolare superiore) li si provino sul sistema che ha la seguente
matrice aumentata, e soluzione esatta
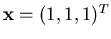 .
.
 Esercizio 3
Esercizio 3
- Usando la doppia precisione, si scriva una subroutine per il calcolo della fattorizzazione LU di Crout
(sezione 4.17.5 del libro di testo).
-
Si scriva poi un programma che calcoli le matrici L ed U di Gauss (senza pivoting)
e quelle
di Crout, provandolo con la matrice dell'Esercizio 2, e verificando che i prodotti restituiscano
la matrice A.
 Esercizio 4
Esercizio 4
-
Usando la doppia precisione,
si scrivano due procedure per implementare la risoluzione di
un sistema con i due metodi di Jacobi e di Gauss-Seidel (sezioni 4.17.6 e 4.17.7 del libro di testo)
-
Si scrivano poi due programmi di utilizzo di tali procedure e si
provino sul sistema:
Si prenda come vettore iniziale
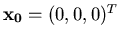 e si determinino
le iterazioni necessarie ad ottenere una tolleranza sulla norma euclidea
del residuo di
e si determinino
le iterazioni necessarie ad ottenere una tolleranza sulla norma euclidea
del residuo di 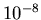 . Si disegnino poi su di uno stesso grafico,
per ogni iterazione
. Si disegnino poi su di uno stesso grafico,
per ogni iterazione 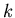 i valori
i valori
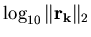 per
il metodo di Jacobi e per quello di Gauss Seidel.
per
il metodo di Jacobi e per quello di Gauss Seidel.
Soluzione: Entrambi i metodi convergono qualsiasi sia la scelta iniziale
di
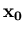 , alla soluzione
, alla soluzione
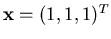 . Perchè?
. Perchè?
Posto
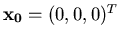 Jacobi converge in circa 34 iterazioni
(
Soluzione Jacobi)
e
Gauss-Seidel (
Soluzione Gauss Seidel)
in circa 16 iterazioni. Il disegno di
Jacobi converge in circa 34 iterazioni
(
Soluzione Jacobi)
e
Gauss-Seidel (
Soluzione Gauss Seidel)
in circa 16 iterazioni. Il disegno di
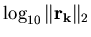 mostra la convergenza più rapida del
metodo di Gauss Seidel.
mostra la convergenza più rapida del
metodo di Gauss Seidel.
 Esercizio 5
Esercizio 5
-
Si consideri il sistema lineare che ha la seguente matrice aumentata (tali
dati devono essere memorizzati su di un file di nome matrice.dat)
- Utilizzando il metodo di Gauss senza pivoting, si calcolino
le due matrici
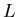 ed
ed 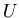 della fattorizzazione
della fattorizzazione 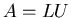 ed il vettore
ed il vettore 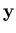 e si scrivano tali dati su di un file di nome gauss.dat.
e si scrivano tali dati su di un file di nome gauss.dat.
Soluzione: gauss.dat
- Utilizzando la fattorizzazione di Gauss-Crout si calcolino le due matrici
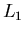 ed
ed 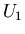 della fattorizzazione
della fattorizzazione 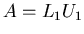 e si scrivano tali dati su di un file di nome crout.dat
(l'ultima colonna della matrice aumentata non deve essere usata).
e si scrivano tali dati su di un file di nome crout.dat
(l'ultima colonna della matrice aumentata non deve essere usata).
Soluzione: crout.dat
 Esercizio 6
Esercizio 6
- Si risolva l'esercizio 4.6 (pag.160 del testo).
 Esercizio 7
Esercizio 7
- Si risolva l'esercizio 4.7 (pag.160 del testo).
 Esercizio 8
Esercizio 8
 Esercizio 9
Esercizio 9
-
Si consideri il sistema lineare che ha la seguente matrice aumentata, e la cui soluzione
esatta è
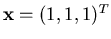
- Dopo aver memorizzato nel file mat2.dat la matrice A, il termine noto
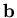 ed il vettore
ed il vettore
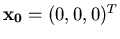 ,
si applichi tre volte il metodo di risoluzione iterativo SOR che converge
sempre se
,
si applichi tre volte il metodo di risoluzione iterativo SOR che converge
sempre se
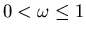 .
.
Perchè? (si scriva la ragione di tale affermazione):
Soluzione: E' una matrice strettamente
diagonale dominante.
Si usi
il test di arresto sulla norma euclidea del vettore residuo
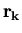 ,
,
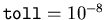 e
e 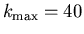 .
Per il parametro
.
Per il parametro 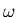 , si utilizzino i tre valori
, si utilizzino i tre valori
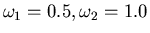 e
e
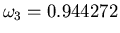 , scrivendo
sui file omega1.dat, omega2.dat e omega3.dat i valori
, scrivendo
sui file omega1.dat, omega2.dat e omega3.dat i valori
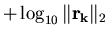 ottenuti con la successione di iterate
e con i diversi valori assegnati ad
ottenuti con la successione di iterate
e con i diversi valori assegnati ad
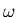 .
.
- Si rappresentino su di uno
stesso grafico, considerando come
ascisse gli indici
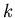 delle iterate, le curve corrispondenti ai valori
delle iterate, le curve corrispondenti ai valori
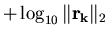 , verificando che il valore
, verificando che il valore 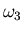 è
quello a convergenza più rapida. Si memorizzi tale figura nel file sorres.ps.
è
quello a convergenza più rapida. Si memorizzi tale figura nel file sorres.ps.
Soluzioni:
mat2.dat,
omega1.dat, omega2.dat, omega3.dat
e sorres.ps
 Esercizio 10
Esercizio 10
 Esercizio 11
Esercizio 11
 Esercizio 12
Esercizio 12
 Esercizio 13
Esercizio 13
-
Si consideri il seguente sistema lineare
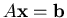 la cui soluzione
è
la cui soluzione
è
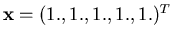 (matrice e termine noto devono essere memorizzati e fatti leggere da un file
di nome sistema.dat)
(matrice e termine noto devono essere memorizzati e fatti leggere da un file
di nome sistema.dat)
- Prendendo come vettore iniziale
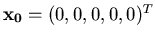 ,
si applichi il metodo iterativo SOR, utilizzando
il test di arresto sulla norma euclidea del vettore residuo
,
si applichi il metodo iterativo SOR, utilizzando
il test di arresto sulla norma euclidea del vettore residuo
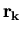 ,
,
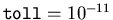 e
e 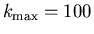 .
Per il parametro
.
Per il parametro 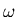 , si utilizzino due valori
, si utilizzino due valori 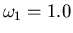 (ovvero Gauss-Seidel) ed
(ovvero Gauss-Seidel) ed
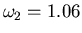 , scrivendo
sui file omega1.dat e omega2.dat i valori
, scrivendo
sui file omega1.dat e omega2.dat i valori
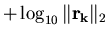 ottenuti con la successione di iterate
e con i due valori assegnati ad
ottenuti con la successione di iterate
e con i due valori assegnati ad
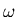 . Alla fine di ciascun file si scrivano anche i seguenti dati:
. Alla fine di ciascun file si scrivano anche i seguenti dati:
Tolleranza
Tolleranza *
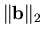
Numero di iterazioni eseguite
Vettore soluzione 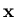
Norma residuo finale
- Si rappresentino su di uno
stesso grafico, considerando come
ascisse gli indici
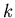 delle iterate, le curve corrispondenti ai valori
delle iterate, le curve corrispondenti ai valori
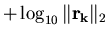 , verificando che il valore
, verificando che il valore 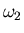 è
quello a convergenza più rapida. Si memorizzi tale figura nel file sorres.ps.
è
quello a convergenza più rapida. Si memorizzi tale figura nel file sorres.ps.
Soluzioni:
sistema.dat,
omega1.dat, omega2.dat e sorres.ps
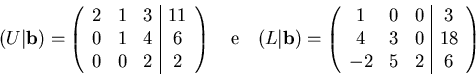
 Esercizio 1
Esercizio 1
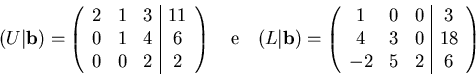
 Esercizio 2
Esercizio 2
 Esercizio 3
Esercizio 3
 Esercizio 4
Esercizio 4
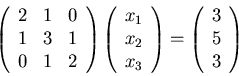
 Esercizio 5
Esercizio 5

 Esercizio 6
Esercizio 6
 Esercizio 7
Esercizio 7
 Esercizio 8
Esercizio 8

 Esercizio 9
Esercizio 9
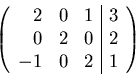
 Esercizio 10
Esercizio 10

 Esercizio 11
Esercizio 11

 Esercizio 12
Esercizio 12

 Esercizio 13
Esercizio 13