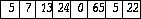

 Parallel Computer Centre
Parallel Computer Centre
An array is a collection of (scalar) data, all of the same type, whose individual elements are arranged in a regular pattern.
There are 3 possible types of arrays depending on the binding of an array to an amount of storage.
Static arrays: their size is fixed when the array is declared and can not be altered during execution. This is inflexible for certain circumstances (one has to re-entry the program, change the dimension(s) and re-compile) and wasteful in terms of storage space (since one might declare a very large array to avoid the previous problem)
Semi-dynamic arrays: the size of an array is determined after entering a subroutine and arrays can be created to match the exact size required but can only be used for a subroutine. In Fortran90 such arrays are called assumed-shape, and automatic arrays
Dynamic arrays : the size and therefore the amount of storage used by a dynamic array can be altered during execution. This is very flexible but slow run-time performance and lack of any bound checking during compilation. In Fortran90 such arrays are called allocatable arrays.
The reasons for using an array are:
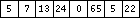
Assuming at the moment that the index (or subscript) starts at 1 then:
Vector: An array with a rank of one is called a vector.
Matrix: An array with a rank of 2 or greater is called a matrix
Consider again the following array: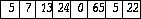
This array represents a vector since it is one-dimensional.
Consider the following array: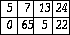
This array represents a matrix since it is two-dimensional.
The term Bounds refers to the lower subscript in each dimension. Hence the vector above has a lower bound of 1 and a higher bound of 8, whereas the above matrix has 1 and 2 for the first dimension and 1 and 4 for the second dimension.
The term Extent refers to the number of elements in a dimension. Hence the above vector has an extent of 8, whereas the above matrix has an extent of 2 and 4 in each dimension.
The term Shape is a vector containing the extents of an array. Hence the above vector has a shape of [8] whereas the matrix has a shape of [2,4].
The term Size refers to the total number of elements of an array, which simply is the product of extents. The size of an array may be zero but more about this later. Both vector and matrix above have a size of 8.
The term Conformance refers to arrays that have the same shape. This is a condition for array to array operations. Obviously an operation between an array and a scalar satisfies the conformance criterion. In such a case the scalar operation is repeated for all the elements of the array, as shown later.
The name given to the array (e.g. Student_mark). The name given to the array is up to 31 alphanumeric characters including underscore but the first character must be a letter.
The type of the elements (e.g. integer). All elements must be of the same type and the type can be integer, real, logical, character, or derived.
The dimensions of the array (e.g. 1 dimension). Up to 7 dimensions are allowed
The lower and upper bounds for each dimension (e.g 1 and 8). Declaring the lower bound is optional. If the lower bound is not specified Fortran90 assumes that the index begins with 1. Notice that the type of the bounds is always integer. The alternate and equivalent forms used to declare an array are as follows:
type, DIMENSION(bound) [,attr] :: name
type [,attr] :: name (bound)
where [,attr] allows for the declaration of other type attributes, if required.
The following declarations are equivalent. Both declare an integer array a with 6 elements; an array b with 10 real elements and a logical 2-dimensional array named yes_no.
INTEGER, DIMENSION(6) :: a
REAL, DIMENSION(0:9) :: b
LOGICAL, DIMENSION(2,2) :: yes_no
INTEGER :: a(6)
REAL :: b(0:9)
LOGICAL :: yes_no(2,2)
Use the dimension attribute form when several arrays of the same bounds and type need to be declared. Use second form when several arrays of the same type but different bounds need to be declared. The choice is influenced by the style followed by the programmer but certain circumstances might dictate the use of one form rather than another.
A mixture of the two forms in the same program is allowed. Some further examples are shown below:
INTEGER, DIMENSION(8) :: x,y
REAL:: alpha(1:3), beta(4:9)
REAL, DIMENSION(0:5,12:45,6) :: data
CHARACTER(len=10) :: names(25)
The first example declares two arrays of the same dimension and type, therefore the dimension attribute form is employed. The second example declares two arrays of the same type but different dimension hence the array specification form is followed. For the third and fourth examples any of the two forms could have been used. The fourth example declares an array which has 25 elements with each element having a character string of size 10.
It is possible to include arrays as components of a derived data type and to declare arrays of derived data types, for example:
TYPE(point)
REAL :: position(3)
TYPE(point)
TYPE(point) :: object(10)
The type point is comprised of 3 real numbers, while the array object consists of 10 items of data, each consisting of 3 real numbers. Components are accessed as follows:
object(1)%position(1) !position 1 object 1
object(7)%position(2:) !positions 2 and 3 object 7
object(4)%position(:) !positions 1, 2 and 3 object 4
object(1:5)%position(1) !illegal object not array section.
Note that the array object cannot be used as an array section, although its components can (this is due to the unconventional storage requirements used by derived data types).
A third form is a mixture of the two above, as shown below:
type, DIMENSION(bound1) [,attr] :: aname, bname(bound2)
where aname takes the `default' number of elements, but bname takes another explicitly defined value. This is still legal but avoid using it due to the confusion that might arise.
array (index, [...])
a(5) refers to the fifth element of the array
b(4,2) refers to the element at the intersection of the 4th row and 2nd column.
For above examples assume that lower bound is 1 and use the following declarations:
REAL, DIMENSION(8) ::a
INTEGER, DIMENSION(5,4) ::b
array ([lower]:[upper]:[step], [...]) where lower and upper default to the declared dimensions and step defaults to 1.
a(3:5) refers to elements 3, 4, 5 of the array
a(1:5:2) refers to elements 1, 3, 5 of the array
b(1:3, 2:4) refers to elements from rows 1 to 3 and columns 2 to 4.
Using colon: This is a facility that enables us to access whole or parts of columns or rows. For example, b(:4) refers to all elements of the fourth column.
Using subscripts: For example, alpha(i,j) refers to the element at the intersection of ith row and jth column. Subscripts i,j are defined previously within the program.
Using expressions: For example, alpha(2*k) refers to an element whose position is the result of the multiplication. The result of an expression must be an integer within the declared bounds.
Using stride: For example, beta(3,1:7:2) refers to elements 1,3,5,7 of the third row., beta(1,2:11:2) refers to elements 2,4,6,8,10 of the first row. This is a valid statement despite that the upper bound of the second dimension is 10.
REAL, DIMENSION(9) :: a
INTEGER, DIMENSION(3) :: random
random=(/6,3,8/)
a(random)=0.0
a((/7,8,9/))=1.2
Here two arrays have been declared, a with size 9 and random with size 3. The third statement assigns the values of 6, 3, and 8 to the three elements of random. Whatever value existed beforehand now has been overwritten. Hence,
random(1)=6
random(2)=3
random(3)=8
The fourth statement uses random as an array of indices and assigns the value of 0.0 to the array elements of a. Expanding the left hand side we get
a(random)=a(random(1),random(2),random(3))=a(6,3,8)
Hence the third, sixth and eighth element of a are the ones being overwritten with a zero value.
The fifth statement demonstrates an alternative use of the vector subscript. Hence the 7th, 8th and 9th element of the array are assigned the value of 1.2
Care must be taken not to duplicate values in a vector subscript when used in the LHS of an expression as demonstrated with the illegal fourth statement below.
REAL, DIMENSION(5) :: a
INTEGER, DIMENSION(3) :: list
list=(/2,3,2/)
a(list)=(/1.1, 1.2, 1.3/) !illegal element 2 set twice
The array element ordering: It is wrong to assume that two elements of an array are next to each other BUT conceptualise a linear sequence of the array elements with the first index changing first.
Consider the following example:
REAL, DIMENSION(3, 5) :: a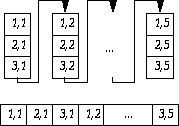
Consider the following example:
REAL, DIMENSION(100) :: a, b, c
REAL : d(10,10) = 0.0
b=2*a+4
a=2.0
c=b*a
c=d
The first assignment involves an array expression on the right hand side. Since a and b are conformable it is a valid statement. Each element of b takes the corresponding value of a multiplied by 2 and adding a 4 to the product.
The second assignment involves a scalar on the right hand side, hence there is automatic conformability. Each element of a takes the value of 2.
The third assignment involves an array product on the right hand side. Since a and b are conformable then their product can be evaluated. The product refers to element by element multiplication. The result is another array which is conformable with c therefore each element of c takes the product of the corresponding elements in a and b.
The fourth assignment is illegal because the two arrays are not conformable.
Consider the following example:
REAL, DIMENSION(10) :: alpha, beta
REAL :: gamma(20)
alpha(1:5)=2.0
alpha(1:10:2)=beta(1:5)/6
alpha(2:10)=alpha(1:9)
gamma(11:20)=beta
The first assignment simply assigns the value of 2 to the first 5 elements of alpha, the rest of the elements remain intact.
The second assignment involves two conformable array sections, hence it is a valid statement. The following assignments are made:
alpha(1)=beta(1)/6
alpha(3)=beta(2)/6
alpha(5)=beta(3)/6
alpha(7)=beta(4)/6
alpha(9)=beta(5)/6
The third assignment shows a powerful operation using arrays where values are shifted automatically and without the need of DO loops. Therefore, the 9 elements of alpha starting from the second element take the value of the first 9 element of alpha, so at the end of the process the first two elements of alpha have the same value.
The last assignment demonstrates another important concept. Whereas beta and gamma are not conformable the section used by gamma satisfies the criterion so it is a valid statement.
Consider the following example:
REAL, num REAL, DIMENSION(3,3) :: a
INTEGER ::length(5)
CHARACTER(len=7) :: c(5)
x=SQRT(num)
a=SQRT(a)
length=LEN( TRIM(c) )
The first assignment is between two scalars and assigns the square root of num to x.
The second assignment involves the same elemental intrinsic procedure but with an array argument. Hence, every element of a is substituted by the square root of the existing value.
The third assignment finds the string length for each element of c and rejects any trailing blanks. Hence, if c(1) is `Alexis ` the command ignores the trailing blank.
INTEGER :: a(5)=(/1,2,1,1,3/)
a(1:count(arr==1))=0
a(1:count(arr==1))=0
The first statement initialises a to 1 2 1 1 3 values.
The second statement arr(1:count(arr==1))=0 will change 1,2,1,1,3 to 0,0,0,1,3 since the original array had 3 elements with the value of 1.
The third statement arr(1:count(arr==4))=0 will do nothing because it is a zero-sized array (lower bound is 1, higher bound is 0 since there are no elements with the value of 4). Allowing for zero-sized arrays means that if the original array is empty or contains no elements with the required value the statement becomes a do nothing statement.
a list of values of the appropriate type:
INTEGER :: a(6)=(/1,2,3,6,7,8/)
variable expression(s)
REAL :: b(2)=(/SIN(x),COS(x)/)
array expression(s)
INTEGER :: c(5)=(/0,a(1:3),4/)
implied DO loops
REAL :: d(100)=(/REAL(i),i=1,100/)
The constructor can be used during declaration as shown above or in a separate statement but only the latter form can be employed to initialise an array with constant values.
RESHAPE (list, shape [,PAD] [,ORDER])
where list is a 1-dimensional array or constructor containing the data, and shape a 1-dimensional array or vector subscript containing the new shape of the data.
The size of the array determines the dimension of the new array. The elements determine the extent of each dimension. Consider the following example:
INTEGER, DIMENSION(2,3) :: a
a=RESHAPE((/i,i=0,5/),(/3,2/))
The last statement will generate a rank 2 array with extents 3 and 2.
The format is:
DATA variable / list / ...
For example see following:
INTEGER :: a(4), b(2,2), c(10)
DATA a/4,3,2,1/
DATA a/4*0/
DATA b(1,:)/0,0/ DATA b(2,:)/1,1/
DATA (c(i),i=1,10,2/5*1/ DATA (c(i),i=2,10,2)/5*2/
The first DATA statement uses a list by value where the value for each array element is explicitly declared.
The second DATA statement uses a list by whole array where 4 is the size of the array and 0 is the required value which is repeated 4 times. Do not confuse this with the multiplication operator.
The third and fourth statements use a list by section where the first row takes 0 0 and the second row takes the values of 1 1.
The last two statements use a list by implied DO loops where the odd indexed elements are assigned the value 1 and the even indexed elements take the value of 2.
Remember that:
The WHERE statement allows a single array assignment only if a logical condition is true. The syntax is as follows:
WHERE (condition) statement
Consider the following situation:
INTEGER :: a(2,3,4)
WHERE(a< 0) a=0
WHERE(a*3>10) a=999
The first WHERE statement means that all negative values of`a are set to zero, the non-negative values of a remain intact.
The second WHERE statement means that elements of a are set to 999 if the product is greater than ten.
The WHERE construct allows array assignment(s) only if a logical condition is true, and alternative array assignement(s) if false. The syntax is as follows:
WHERE (condition)
block1
[ELSEWHERE
block2]
ENDWHERE
Examine the following section of a program.
INTEGER :: b(8,8)
WHERE (b<=0)
b=0
ELSEWHERE
b=1/b
ENDWHERE
So all negative valued elements of `b' are set to zero and the rest take their reciprocal value.
ALL (condition, [DIM])determines whether all elements along a given dimension (DIM) satisfy the condition. The outcome is either a scalar (if dimension part is missing) or an array (if dimension part is declared) of logical type.
LOGICAL :: test, test2(2), test3(3)
REAL, DIMENSION(3,2) :: a
a = (/5,9,6,10,8,12/)
...
test=All(a>5)
test2=All(a>5, DIM=1) !false, true, true
test3=All(a>5, DIM=2) !false, true
The first statement gives false since the first element is equal to 5 and not greater.
The second statement gives [false,true,true] since the first element of the first row is equal to 5 and not greater, whereas both elements on the remaining two rows are greater than 5.
The third statement gives [false,true] since first element of the first column is equal to 5 and not greater, whereas all 3 elements on the remaining column are greater than 5.
SIZE(array, [DIM])returns the extent of an array for the specified dimension (DIM). If the dimension part is missing it returns the total number of elements in the array.
REAL, DIMENSION(3,2) :: a
num=Size(a)
num=Size(a,DIM=1)
num=Size(a,DIM=2)
The first statement gives 6, the second gives 2, and the last gives 3.
SPREAD(array, DIM, NCOPIES)replicates the given array by adding a dimension, where DIM stands for dimension and NCOPIES for number of copies.
REAL, DIMENSION(3) :: a=(/2,3,4/)
REAL, DIMENSION(3,3) :: b,c
b=SPREAD(a, DIM=1, NCOPIES=3)
c=SPREAD(a, DIM=2, NCOPIES=3)
The first SPREAD statement replicates array a three times on the row dimension. The second SPREAD statement replicates array a three times on the column dimension.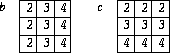
MAXLOC(array, [mask])determines the location of the first encountered element of the given array which has the maximum value and satisfies the optional mask.
REAL :: a(5) a=(/2,8,5,3,4/)
num = MAXLOC( a )
num = MAXLOC( a, MASK=a<5 )
num = MAXLOC( a(2:4) )
The first MAXLOC statement returns 2 since this is the position of the highest number on the list.
The second MAXLOC statement returns 5 since this is the position of the highest number on the list when numbers greater than 5 are excluded.
The third MAXLOC statement returns the value 1 since this is the position of the highest valued element in the array section. Note that it is worth remembering that elements in array section statements are renumbered with one as the lower bound in each dimension.
(a) A user enters the following elements to a (3x3) array: 1, 2, 5,8, 6, 7, 5, 0 , 0. What is the value of element(2,1); (3,2); (1,2); (2,3).
(b) An array with rank 7 and extent of 5 in each dimension, how many elements does it have?
(c) An array with rank 3 and extents of 10, 5 and 3, how many elements does it have?
REAL, DIMENSION(1:10,1:20) :: a
REAL, DIMENSION(10,-5:10) :: b
REAL, DIMENSION(0:5,1:3,6:9) :: c
REAL, DIMENSION(1:10,2:15) :: d
What is the rank, size, bounds, and extents of a,b,c and d?
REAL, DIMENSION(-1:5,3,8) :: alpha
REAL, DIMENSION(-3:3,0:2,-7:0) :: beta
Are the two arrays conformable?
REAL: a(0:5,3)
which of the following references are legal?
a(2,3), a(6,2), a(0,3), a(5,6), a(0,0)
INTEGER, DIMENSION(-1:1,2,0:1) :: alpha
5 6
4 2
0 5
0 0 0 1
0 0 1 1
0 1 1 1
REAL, DIMENSION(50) :: alpha
REAL, DIMENSION(60) :: beta
which of the following statements are valid?
alpha=beta
alpha(3:32)=beta(1:60:2)
alpha(10:50)=beta
alpha(10:49)=beta(20:59)
alpha=beta(10:59)
alpha(1:50:2)=beta
beta=alpha
beta(1:50)=alpha
(a) a constructor with the list of values
(b) a constructor with the Do Loop
alpha(/-1,(0,i=2,49),1/)
alpha((/-1,(0,i=1,48),1/)
alpha((/-1,(0,i=37,84),1/)
alpha(/-1,48*0,1/)
REAL, DIMENSION(2,2) ::delta=Reshape((/((10*i+j,i=1,2),j=1,2)/), (/2,2/))
INTEGER, DIMENSION(10) :: beta
what elements are referenced by each of the following statements?
beta(2:8:3)
beta(1:10)
beta(3:5)
beta(:9)
beta(:)
beta(::4)
beta(3:10:0)
REAL, DIMENSION(3,4) : gamma
what elements are referenced by each of the following statements?
gamma(2,:)
gamma(:,3)
gamma(2,3:4)
gamma(::2,:)
INTEGER, DIMENSION(-5:0) :: alpha=(/2,18,5,32,40,0/)
what is the result of
MAXLOC(alpha)
MAXLOC(alpha,MASK=alpha/=40)